概念說明
股票市場上的股價指數會有開盤、最高、最低和收盤,個股也是如此。如果要做預測股價指數就需要先將股價指數的數字規律表現出來,然後再估計股價指數的數學模式,也就是建模。如果能夠愈精準,離預測就會更近一步。
建模技術需要依賴機率論、統計、數理統計、數學,還有計量經濟學針對當數據集不符合迴歸分析時的討論項目。只是計量經濟學內容是以檢定為主。檢定是在顯著水準下做二分法的選擇,但對於建模來說並沒有什麼幫助,因為建模就是要愈準愈好。
從一開始所有人都知道股價指數和很多商品價格一樣都是非線性的時間序資料,只是股價指數的走勢更為混亂,所以很多人都認為股價指數更難以被有效建模。
現在,我們將建模技術公開給各位,了解這樣的新知識。每個指數會依照
三個項目進行解析盤勢,讓各位了解由高中數學和大學學習的統計相關知識就可以分析股市,這些數字也具有其意義。
以開盤指數為說明例子
1. 歷史資料看走勢
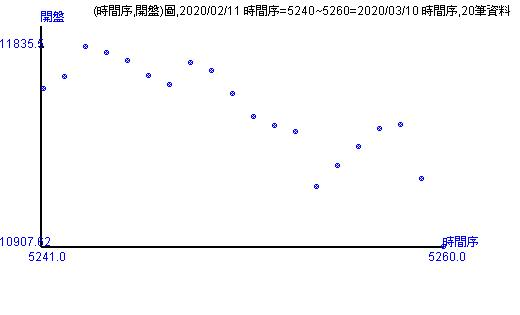
歷史資料的走勢有20天、50天、100天、200天。由股價指數走勢圖可以看出幾個重點:
- 新加入的看開盤指數會出現在最右邊,並且是20和50天以來的最低點。
- 從不同天數上,可以看出開盤指數的數字群。例如,20天有兩群數字群,最右邊的數字很有線性上漲後再直線下跌。你可以跟著圖形自己畫出數字群。
- 畫完數字群後,可以看其走勢,也可以看全體走勢。走勢圖可以看出目前台股的現況與可能走的方向。
20個交易日開盤走勢圖
50個交易日開盤走勢圖
100個交易日開盤走勢圖
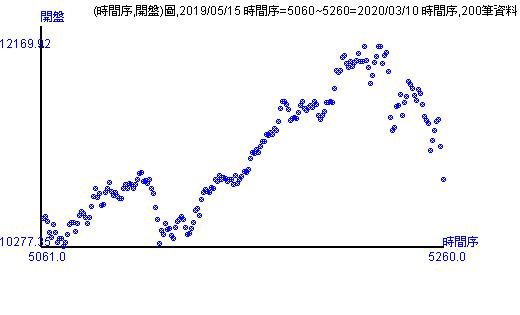
200個交易日開盤走勢圖
上方的走勢圖都是種「點圖」。台灣喜歡用K線圖,美國的彭博網站或是YAHOO財經對股價指數或股價的呈現方法就是「線圖」。線圖跟點圖很像,線圖是將點連上成線。
只是用「線圖」表示還是有問題。因為「開盤指數」或「開盤價」是發生每天的開盤當下,兩天之間是不會有開盤的數字出現,如果用線圖表示代表線的地方都是有數值的!
用K線圖表示則是代表當日的四個指數位置狀態,如同統計學課本中的箱形圖出現最高、最低、第一二三分位數。K線圖則是顯示當日開盤、最高、最低和收盤的位置狀態。
對走勢或趨勢的表現,通常都是用線圖或點圖,不會有人用箱形圖。因此跟箱形圖概念一樣的K線圖其實不適合做為顯示股價指數或股價的走勢或趨勢圖。這裡就選擇用點圖表示開盤在圖形當中的時間段所表現的走勢情況。
2. 預測先估計再算預測區間
2.1. 估計平均線
在發展最新科技的技術時,總要有理論基礎。估計是統計學的方法,所以我們就得先做迴歸分析。但在做迴歸分析時,歷史資料走勢顯示是非線性,所以肯定不能用線性模式去做!
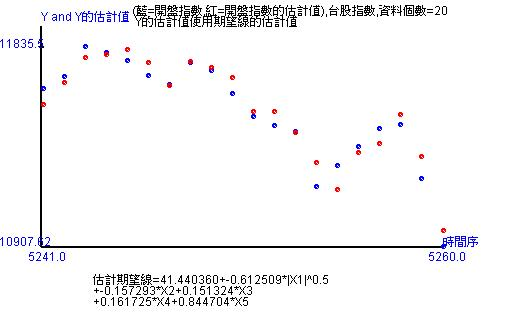
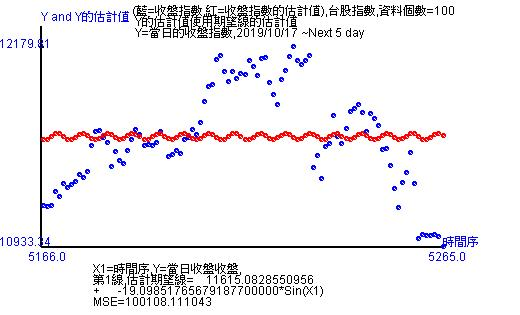
使用非線性模式估計,天數20天、50天、100天、200天、2000天,或更細的天數。紅點是估計值,藍點是實際值。紅點和藍點愈是重合,代表估計得愈準確。另外,圖形下方有估計方程式。由於估計方程式是種轉換方程式,所以當日開盤是受到開根號的時間變數、開盤、最高、最低、收盤影響。
當時間拉長到過去的2000筆歷史數據,經過估計,可以看出紅點幾乎重合於藍點,並且有些藍點還是無法被估計到。
2.2. 預測區間
在統計學的作法上,想要得到預測區間或是做區間估計,其概念為
1. 找點估計量的抽樣分配,確定點估計量的平均數和標準差
2. 設定可信度(信賴水準),找到母體平均數的區間上下限
3. 上下限是由樣本的平均數、標準差、樣本個數、抽樣分配臨界值組成
預測區間則是迴歸分析時會提到。這裡的方法就是迴歸分析,所以預測區間一樣可以做到。但是估價指數或股價的預測區間都沒有出現的原因是一開始點估計就要準!不準的話,區間估計就不要談了,更何況預測區間。前面已經有平均線的估計,可以看出準確程度。
(點估計量)當時間序的數字選擇03/11對應的數字,其他自變數選擇03/10的開盤、最高、最低、收盤,就可以找出03/11開盤指數的預測值。
不過,為了提高估計模型準確度,股價指數是在估計平均線上下波動,也就是有異動情況(變異數異質性)。當然也要將之估計出來,納入模型中。以平均絕對離差代表異動程度,經過估計就可以找出異動程度。最後股價指數前後期會有影響,例如今天漲,明天會跟著漲的情況很常見。所以前後期的關係可以由**自動相關係數**抓到,形成誤差的一階自我迴歸模型。後面兩個部分都是在計量經濟學當中出現的,各位可以參考計量經濟學的書籍。
預測區間的計算方法就依賴前二個模型組合在一起後,可以得到殘差*。而平均絕對離差還原過程會產生正值或負值,這也對應股價指數會上漲或下跌概念。這很類似Parabolic Stop and Reverse (SAR)拋物線指標。不同之處在於
1. 此處的使用方法有理論基礎 - 變異數異質性
2. 平均絕對離差的正負值還原,決定上漲還是下跌的異動程度計算
3. 標準預測區間計算方法做預測用,不是落後
所以可以得到95%預測區間並且可分為上漲設定、下跌設定和全體資料納入的預測區間。
1. 事前:如果你覺得會繼續上漲就可以看上漲設定的預測區間
2. 事後:可以測定開盤是落於上漲設定還是下跌設定的預測區間
圖形紅點是上限,黃點是下限,藍點是實際值。其意義有
1. 最右邊是明日的預測區間,可以定錨,讓人心裡有底,知道明日開盤大約落在哪
2. 右邊像左第二個是看今天的開盤。如果落在預測區間內代表有抓到開盤,也代表歷史數據資訊可以含蓋今日開盤,不出預期。但如果不能被抓到,那就表示超跌或超漲,超過歷史數據的資訊的能力,甚至可能是震盪劇烈。
3. 預測區間的寬度很重要!寬度愈寬表示異動程度愈大,變異數變大,風險提高。
4. 一樣可看出走勢,甚至更清楚!
從上圖可以看出03/11開盤還是會向下走
2.3. 上漲和下跌的大數據分析
這裡的大數據分析就是「意向大數據分析」的應用方法。將股價指數進行分類為上漲和下跌,就可以計算其邊際、條件機率值。透過機率值進行判定。
不過在計算機率之前需要對股價指數做分類與檢定,所以隨機性檢定可得到開盤指數的漲跌是隨機的。然後再用可獲得的歷史數據最大量進行邊際和條件機率計算,提供讀者自行判斷。
其實機率值的計算上,還可以用漲跌數字為權數去調整與計算。所以看到機率值時不要太高興,因為得先了解那些數字是怎麼算出來的,就像拋物線指標,為什麼要那樣設計,以及為什麼要設定0.2,那是否合理等。
-------
最高指數、最低指數、收盤指數也是使用相同的分析方法。請各位前往YouTube頻道和臉書的粉絲專頁看影片和完整資料內容。
-------
台股收盤vs國泰金收盤
比對圖可以顯示股價指數對股價指數、股價指數對個股股價,只要是數字類型的時間序資料都可做此比對。除了走勢比對外,當然股市或股票的「股性」也可以從中看出。那怎麼看股性呢?
藍色:台股收盤;紅色:國泰金收盤
這裡提供樣本相關係數、漲幅比率和上漲:下跌。
所謂樣本相關係數是兩個變數之間的線性關係。
* 如果線性關係高,那相關係數就會非常接近1或-1。
* 如果線性關係很小,他們可能有其他關係,相關係數就會接近0。
* 正值代表兩者有正的線性相關,也就是一個變數數值提高,另一個數值也是提高。
* 負值代表兩者有負的線性相關,也就是一個變數數值提高,另一個就是下降。
* 數值代表線性關係可以解釋的程度
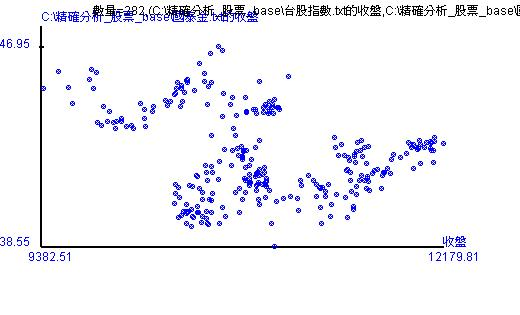
例如上圖是-0.26,代表台股收盤和國泰金收盤有負向的線性相關,也就是台股收盤指數高,國泰金收盤價就低。至於兩者之間的線性程度只有26%,也就是如果看到國泰金收盤走跌,這段期間台股收盤指數有26%上漲可能。至於74%就不屬於線性關係可以解釋的。
台股收盤和國泰金收盤的散佈圖-最後282筆資料
那不同時間區段就會得到不同的相關係數,所以股市或股市、股市或個股的關係不是一句「關係很密切」或「不太有關係」可以概括說明,而是需要這樣的係數值讓投資人判斷。相關係數是在目前高中或高職課本上的概念與公式,現在這邊就可以讓高中生或高職生知道這個係數是這樣使用。
漲幅比率是以這時間區段的 (最後點的收盤指數 - 起始點的收盤指數)/起始點的收盤指數 計算得到。同樣受到不同時間區段影響而有不同數值。這也是報酬率的計算概念。如果投資人是在這段時間投資,就可以計算出買點和賣點的投資報酬率。而軟體都可以自由設定,只是這是做解釋用,提供參考而已。
至於上漲:下跌是計算出這段時間內上漲的個數和下跌的個數,然後以國中教的比例方式呈現。
另外,還有台股收盤和國泰金收盤的散佈圖。試想上面有一條直線,藍點如果非常集中在線的附近,那就代表有高度的線性相關,反之就是低的線性相關。而相關係數的正負值就是代表那個直線是由左上到右下,還是右上到左下。
預測未來5個交易日的台股指數
在預測時是一個預測值而已,所以5個交易日就有5個值。如果只是看下方的數值是沒有意義的。因為對於預測來說,預測愈未來的數值是愈不準的,因為沒有人知道會發生有什麼意外。不過這些數值的參考性還是足夠的,特別是在走勢圖上形成的相對位置比較,讓投資人心中對未來有些概念。所以這些預測值不是用來每日投資使用,而是建立投資人對未來走勢的感覺。
預測值
透過比對紅點的預測值和藍點實際值的位置,可以看出未來的走勢情況,而不是憑空想像。
趨勢圖
所謂的趨勢圖就是以直線、非線性或curvilinear估計得到後所形成的方向。這三種方法當中,直線和非直線估計方法都是可以提供很強烈的方向感,而curvilinear則是做準確使用。
以台股收盤的100天資料進行估計後,非線性模式可以看到是波型的sin函數,所以代表在這100天是震盪波動。
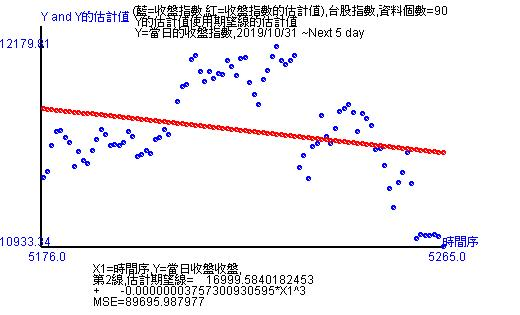
90天的資料再估計後是時間變數的立方函數,同時從線型看出是走下跌趨勢。所謂的立方,就是時間變數值愈大或愈小都會變成極端值。在股價指數上就是暴漲跟暴跌。
當使用20天的資料估計後跟前面不同,方程式由時間的立方轉為時間的倒數。對斜率值有很大的影響。
結語
這是來自YouTube頻道的影片內容。對最難被估計和預測的股價指數,其實那只是數字特性,如果可以了解金融數據為應變數,想了解與其他變數的關聯,就得尋找高線性相關的變數。
第二,時間區段不同就會造成估計、預測、相關係數計算的不同。
第三,比對大盤和個股、大盤和大盤,甚至是其他數字走勢都是沒有問題的,並且姐容易解讀。這是國中的幾何,甚至日常生活就會看到的資訊。至於如何計算直線方程式,或是先將數字轉換,做直線方程式都是根據高中數學技巧。
第四,部分分析技術和知識是大學、研究所才會學習到的。甚至也有最新的科技技術在其中。